根据动态规划原理,最优路径具有这样的特性:如果最优路径在时刻t通过结点\(i_t^*\),那么这条路径从结点\(i_t^*\)到终点是部分路径,对于从\(i_t^*\)到\(i_T^*\)的所有可能路径来说,必须也是最优的。
维特比算法实际是用动态规划解隐马尔科夫模型预测问题,即用动态规划求解概率最大路径(最优路径)。这时一条路径对应着一个状态序列。
根据动态规划原理,最优路径具有这样的特性:如果最优路径在时刻t通过结点\(i_t^*\),那么这条路径从结点\(i_t^*\)到终点是部分路径,对于从\(i_t^*\)到\(i_T^*\)的所有可能路径来说,必须也是最优的。因为假如不是这样,那么从结点\(i_t\)到\(i_T^*\)就有另一条更好的路径存在,如果把它从结点\(i_1^*\)到\(i_t^*\)路径连接起来,就会形成一条比原来路径更优的路径,这是矛盾。依据这一原理,我们只需从时刻t=1开始,递推地计算在时刻t状态为i的各条路径的最大概率,直至得到时刻t=T状态为i的各条路径的最大概率。时刻t=T的最大概率即为最优路径的概率\(P*\),最优路径的\(i_T^*\)也同时得到。之后,为了找到最优路径的各个结点,从终点\(i_t^*\)开始,由后向前逐步求得结点\(i_{T-1}^*, ....,i_1^*\),得到最优路径\(I^* = (i_1^*, i_2^*, ...,i_T^*)\)。
定义两个变量\(\delta\)和\(\Psi\)。定义在时刻t状态为\(i\)的所有单个路径\(i_1, i_2, ...i_t\)中概率最大值为:
\[\delta_t(i) = Max_{i_1,..i_{t-1}} \space P(i_t = i,i_{t-1},...i_1,o_t,...,o_1|\lambda)\] \[i=1,2,3..N\]由定义可得变量\(\delta\)的递推公式:
\[\delta_{t+1}^{i} = max_{i_1,i_2,..i_t} P(i_{t+1} = i, i_t,...,i_1,o_{t+1},...o_1|\lambda)\] \[=max_{1<=j<=N}[\delta_t^{(j)}a_{ji}]b_i(o_{t=1}), i=1,2,,..N; t=1,2,..,T-1\]定义在时刻t状态为i的所有单个路径(\(i_1,i_2,..i_{t-1}, i\))中概率最大路径的第t-1个结点为:
\[\Psi_{t}^{(i)} = arg max _{1<=j<=N}[\delta_{t-1}(j)a_{ji}], i=1,2,...N\]维特比算法推理公式
输入:模型\(\lambda = (A,B,\pi)\)和\(O=(o_1,0_2,...,o_T)\);
输出:最优路径\(I* = (i_1^*, i_2^2,....,i_T^*)\)。
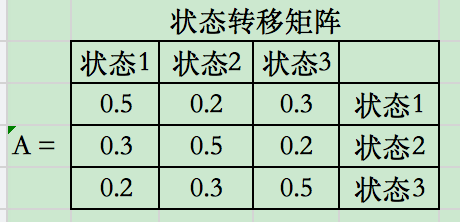
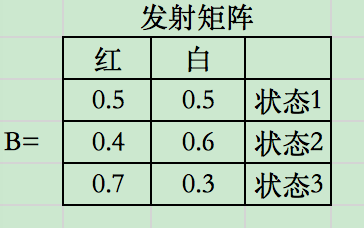
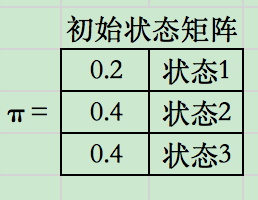
其中\(A: 状态转移矩阵,B: 发射矩阵(给定某状态条件下,观察序列b_i的概率), \Pi: 初始状态概率\)
(1)初始化
\[\delta_1^{i} = \pi_ib_i(o_1), i=1,2,3,N\] \[\Psi_t(i) =0, i = 1,2,3,...N\](2)递推。对t=2,3,…T
\[\delta_t^{(i)} = max_{1<=j<=N}[\delta_{t-1}(j)a_{ji}]b_i(o_t)\] \[\Psi_{t}^{(i)} = arg max _{1<=j<=N}[\delta_{t-1}(j)a_{ji}], i=1,2,...N\](3)终止
\[P^* = max_{1<=i<=N}\delta_T(i)\] \[i_T^* = arg max_{1<=i<=N }[\delta_T(i)]\](4)最优路径回溯
对于t=T-1,T-2,…,1
\[i_t^* = \Psi_{t+1}(i_{t=1}^*)\]求得最优路径\(I^* = (i_1^*, i_2^*,i_3^*,...i_T^*)\)
维特比示例
模型输入\(\lambda = (A, B, \Pi)\),
已知观测序列O=(红白红),求最优状态序列,即最优路径\(I^* = (i_1^*, i_2^*,i_3^*)\)
求解步骤:
(1)初始化。在t=1时。对每一个状态i,i=1,2,3,求状态为i观测\(o_1\)为红的概率,记此概率为\(\delta_1^{(i)}\)
\[\delta_1^{(i)} = \pi_ib_i(o_1) = \pi_ib_i(红), \space i=1,2,3\]带入数据:
\[\delta_1^{(1)} = 0.1\] \[\delta_1^{(2)} = 0.16\] \[\delta_1^{(3)} = 0.28\]以上三值可理解为从t=0时刻到t=1时刻的所有路径中,各个状态下路径结点的最大概率。如,在t=1时,状态为1的路径结点最大概率是0.1。
最大概率路径前一结点:
\[\Psi_1(i) = 0, \space 1,2,3\]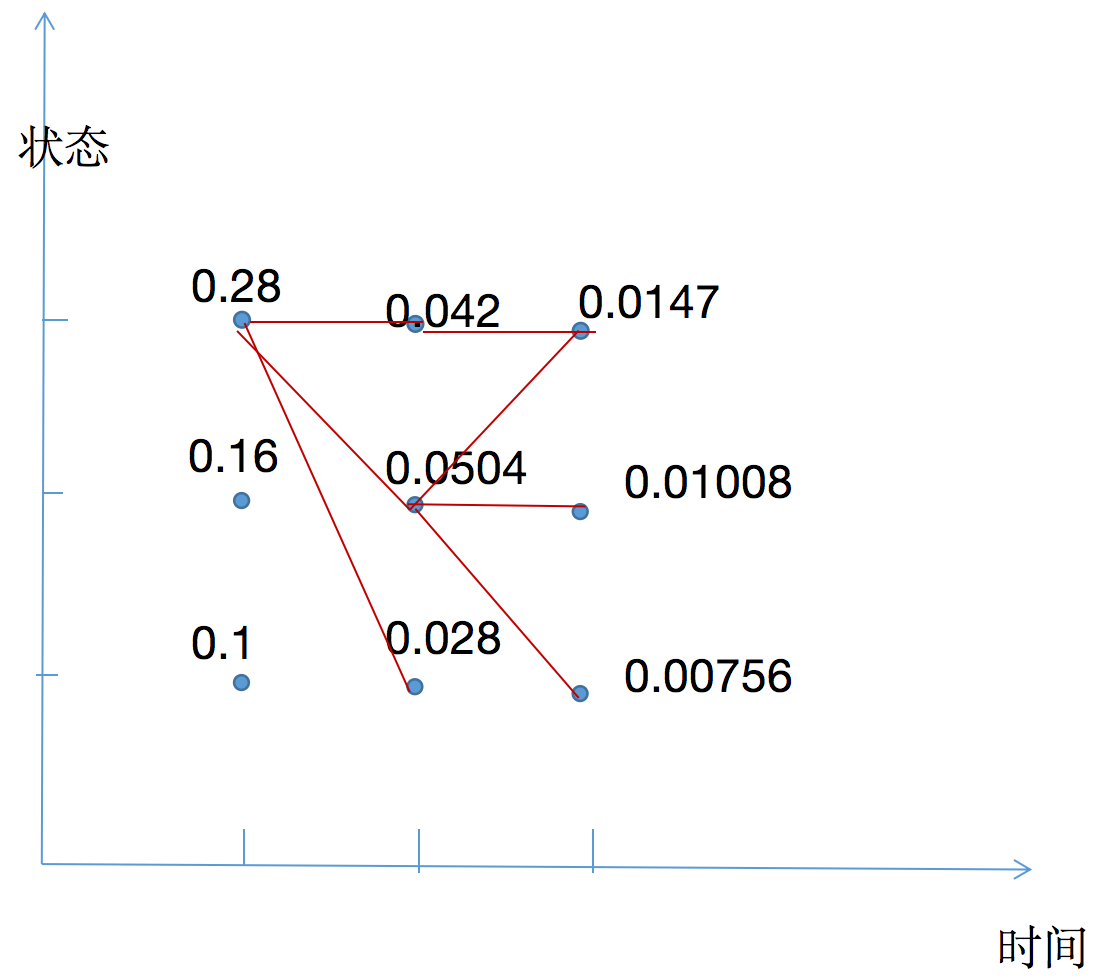
(2)在t=2时,对每个状态i, \(i=1,2,3\),求在t=1时刻状态的j的观测为红并在t=2时刻状态为\(i\)观测\(o_2\)为白的路径的最大概率,记此最大概率为\(\delta_2^{(i)}\),则:
\[\delta_2^{(i)} = max_{1<=j<=3}[\delta_1(j)a_{ji}]b_i(o_2)\]可理解成,前一时刻状态\(j\)的路径最大概率乘上状态由\(j\)转移到状态\(i\)的概率乘上状态\(i\)条件下观测是\(o_2\)的概率。前一时刻状态j存在多个值,选择\(max_{1<=j<=3}[\delta_1(j)a_{ji}]\)值最大者。
同时,对每一个状态i, \(i = 1,2,3\),记录概率最大路径的前一个状态\(j\):
\[\Psi_2^{i} = arg max_{1<=j<=3}[\delta_1(j)a_{ji}], \space i=1,2,3\]可理解成,确定好了当前时刻的最大概率路径的状态\(i\),回溯前一时刻的状态,也就是依据前一时刻到达某状态\(j\)的概率乘上状态\(j\)转移到\(i\)的概率。
计算:
\[\delta_2^{(1)} = max_{1<=j<=3}[\delta_1(j)a_{j1}]b_1(o_2)\] \[=max_j{0.1 * 0.5, 0.16*0.3 , 0.28*0.2} * 0.5\] \[=0.028\] \[\Psi_2(1) = 3\] \[\delta_2(2) = 0.0504\] \[\Psi_2(2) = 3\] \[\delta_2(3) = 0.042\] \[\Psi_2(3) = 3\]同样计算,t=3时:
\[\delta_3^{(i)} = max_{1<=j<=3}[\delta_2(j)a_{ji}]b_i(o_3)\] \[\Psi_3(i) = argmax_{1<=j<=3}[\delta_2(j)a_{ji}]\] \[\delta_3(1) = 0.00756\] \[\Psi_3(1) = 2\] \[\delta_3(2) = 0.01008\] \[\Psi_3(2) = 2\] \[\delta_3(3) = 0.0147\] \[\Psi_3(3) = 3\](3)以\(P^*\)表示最优路径的概率,则:
\[P^* = max_{1<=i<=3}\delta_3(i) = 0.0147\]最优路径终点是\(i_3^*\):
\[i_3^* = argmax_i[\delta_3(i)] = 3\](4)由最优路径的终点\(i_3^*\), 逆向找到
\(i_2^*, i_1^*\) 。
在t=2时,\(i_2^* = \Psi_3(i_3^*) = \Psi_3(3) = 3\)
在t=1时,\(i_1^* = \Psi_2(i_2^*) = \Psi_2(2) = 3\)
贪心算法
在解码阶段,根据输入的文本\(x_1, x_2, ...x_m\)逐个生成单词\(y_1, y_2,...y_n\),整个解码的目标是使得所生成单词序列能够最大化条件语言模型的概率:
\[P(y_1y_2,..y_n|x_1,x_2,x_3,..x_m) = \Pi_{i=1}^{n}P(y_i|y_1,..y_{i-1},x_1,x_2,x3,...x_m)\]从上面公式可以得出。所有可能的单词序列个数是指数级别的,即\(V^n\),如何快速找到最优的单词序列呢?
在上面所讲的维特比动态规划算法,它可以高效的计算出最优的序列。维特比算法定义了数组\(f(i,j)\)表示在所有\(q_i=j\)状态序列中,前\(i\)个单词能达到最大的路径概率值。然而在自然语言生成模型中,模型每一步产生的状态是一个向量,而不是HMM中的K种状态的中的一种。显然,我们不可能定义一个下标是实数向量的数组。
一个可行的办法是使用贪心算法,每一步选择当前可能性最大的单词:
\[y_i = argmax P(w|y_1,y_2,..y_{i-1}, x_1,x_2,..x_m)\]但是这种方法并不能保证全局最优。 例如在第一步中,让
\[P(y_1|x_1,x_2,..x_m)\]最大并不能保证选出的词可以让全局概率
\[P(y_1,y_2,..y_n|x_1,x_2,..x_m)\]最大。 例如,如果给定问题,“他擅长做什么?”正确答案是“他踢球很厉害”。假如贪心算法成功生成第一个词,“他”之后,正在选择第二个词语。而在训练集当中,“他”之后出现“是”的概率远远大于“踢球”的概率,那么经过训练的模型在这一步很可能赋予“是”更大的概率,即\(P(是|他;他擅长什么) > P(踢球|他;他擅长什么)\)。但是选择“是”之后的结果很可能和问题毫无相关,如“他|是|一名|老师”。然而,全局概率
\[P(他|踢球|很|厉害; 他擅长做什么) > P(他|是|一名|老师; 他擅长做什么)\]。因此,贪心算法最大的问题是“短视”,即当前局部最优不一定是全局最优。
集束搜索
集束搜索是解决这个问题的好方法,Beam Search的每一步并不只选取当前概率最大的下一个词,而是选取B个。参数B被称为集束宽度,这样第1步之后算法有了B个最优可能的第1个单词,在第2步时从这B个单词分别寻找最优可能的B个下一个单词,这样可以获得\(B^2\)个序列。在这些序列中选取当前概率最大的B个保留下来,然后继续第三第四步,因此集束搜索每一步都有B个当前保留下来的最优的序列,然后经过模型拓展下一个单词,并保留其中最优的B个。
整个过程中,如果概率最大的前B个最新产生的单词中有</s>,说明对应序列结束,这样可以将这个序列保存。解码过程需要设置生成文本长度限制\(L\),一旦候选序列长度达到\(L\),即终止算法。最后在所有保存下来的输出文本序列中选择全局概率最大的输出。
在集束搜索实践中,由于全局概率\(P(y_1,y_2,..y_n|x_1,x_2,x_m)\)是所有单词条件概率的乘积,因此会出现越长的句子全局概率越小的情况,这会导致算法倾向于挑出最短的句子。常用长度归一化技巧解决这一问题,及使用平均全局概率\(P(y_1,y_2,..y_n|x_1,x_2,x_m) = \frac{P(y_1,y_2,..y_n|x_1,x_2,x_m)}{n}\) 另外集束搜索束大小越大,越可能找到最优的解,但是计算复杂度也会上升,所以集束搜索的束大小的选择需要在模型质量和效率之间寻求平衡。